| Vertical shift |
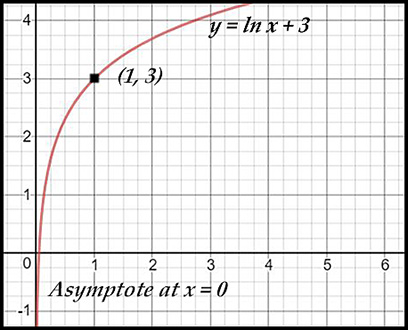
1. y = logex + 3
The curve y = ln x has:
x-intercept at (1, 0).
asymptote at x = 0.
- the + 3 raises the x-intercept of (1, 0) to
(1, 3).
- the new x-intercept is at (e-3, 0).
- the asymptote is unaffected.
|
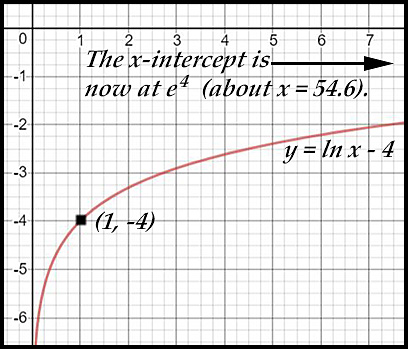
2. y = logex - 4
The curve y = ln x has:
x-intercept at (1, 0).
asymptote at x = 0.
- the - 4 lowers the x-intercept of (1, 0) to
(1, -4).
- the new x-intercept is at
(e4 (= 54.6), 0).
- the asymptote is unaffected.
|
| Expansion/contraction |
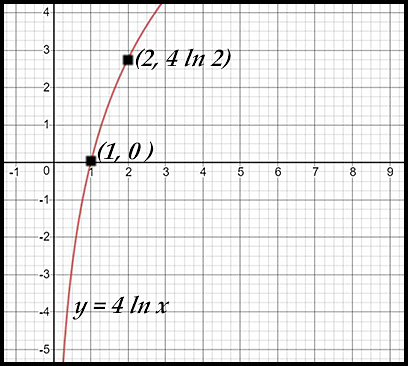
3. y = 4loge x
The curve y = ln x has:
x-intercept at (1, 0).
asymptote at x = 0.
- neither the x-intercept nor the asymptote is affected.
- at x = 2, the new point is (2, 4ln 2).
|
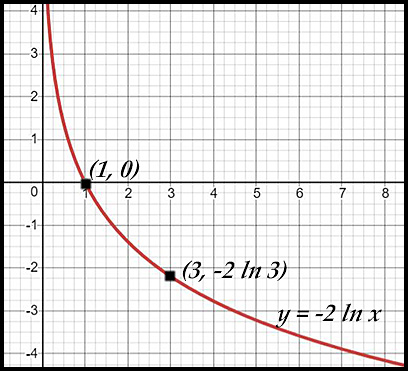
4. y = -2loge x
The curve y = ln x has:
x-intercept at (1, 0).
asymptote at x = 0.
- neither the x-intercept nor the asymptote is affected.
- the negative sign in the original equation shows the asymptote is at large positive values of y.
- at x = 1, the new point is (1, -4) because
ln 1 = 0.
|
| |
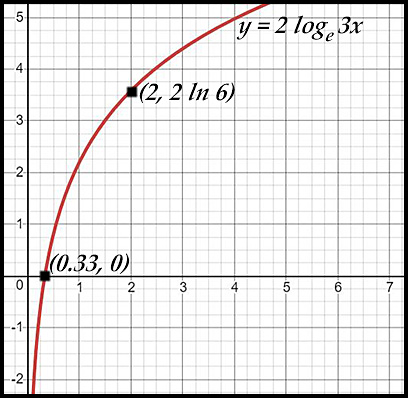
5. y = 2 ln 3x
The curve y = 2ln 3x has:
x-intercept at (0.33, 0) as we put
3x = 1.
asymptote at x = 0.
- the x-intercept reduces to 0.33 (ln 3x = 0 gives 3x = 1) due to the curve increasing proportional to 3 not 1 while the asymptote is unaffected.
- at x = 2, the new point is (2, 2ln 6).
|
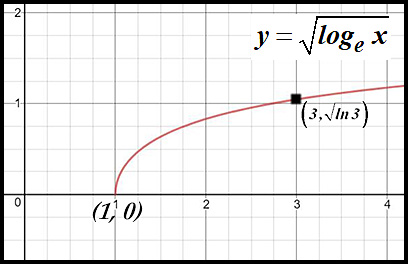
6.

The square root simply reduces all the positive values and eliminates all negative values.
- x-intercept does not change from (1, 0).
- asymptote is removed because we can't take the square root of negative numbers..
- the curve shrinks due to all values being reduced to their square root.
|
| Transformation - combination |
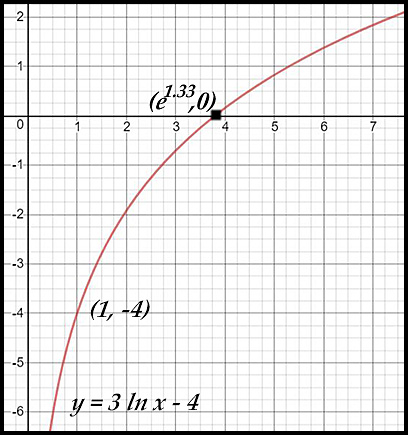
7. y = 3ln x - 4
The curve y = 3ln x - 4 has:
- x-intercept at (e1.33, 0) as we put
y = 0 so
ln x = 4/3 = 1.33.
- asymptote is unchanged at x = 0.
|
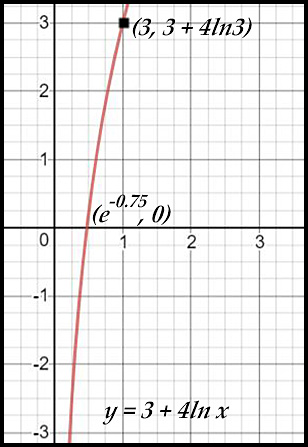
8. y = 3 + 4ln x
The curve y = 3 + 4ln x has:
- x-intercept at (e-0.75, 0) (about x = 0.47) as we put y = 0 so ln x = -3/4 = -0.75.
- asymptote is unchanged at x = 0.
- note how quickly the curve rises compared to the previous question.
|
| |
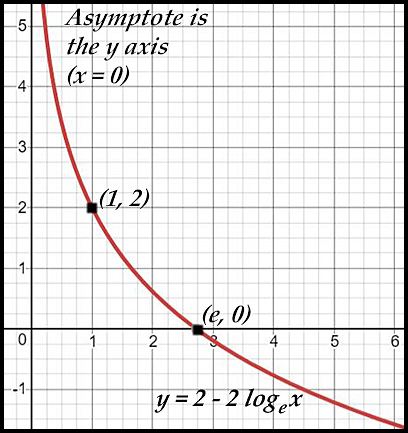
9. y = 2 - 2loge x
The curve y = 2 - 2 ln x has:
- x-intercept at (e, 0) as we put
y = 0 so ln x = 1.
- asymptote is unchanged at x = 0.
- curve comes down from the positive end of the y axis because of the negative in front of the log term.
|
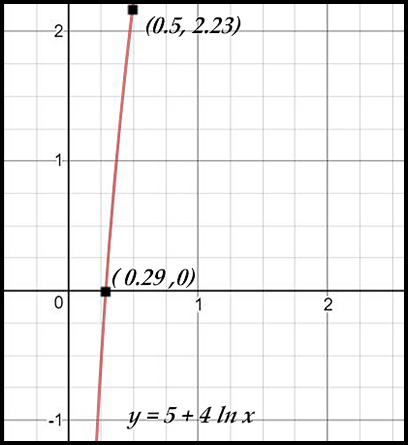
10. y = 5 + 4 loge x
The curve y = 5 + 4loge x has:
- x-intercept at (e-1.25, 0) as we put
y = 0 so ln x = -5/4.
- asymptote is unchanged at x = 0.
|
| Horizontal shift |
11. y = 2 loge (x + 4)
The curve y = 2loge (x + 4) has:
- x-intercept when x + 4 = 1
so at x = -3
.
- asymptote when x + 4 = 0 -
so at x = -4.

|
12. y = loge (3x + 2)
The curve y = loge (3x+2) has:
- x-intercept at (e, 0) as we put
3x + 2 = 1 so x = -1/3 = -0.33.
- asymptote when 3x + 2 = 0
so at x = -2/3 = -0.67
.
- y-intercept when x = 0 (y = ln 2).

|
| |
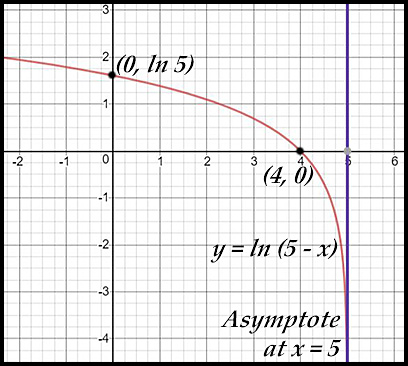
13. y = loge (5 - x)
The curve y = ln (5 - x) has:
- x-intercept when 5 - x = 1 so at x = 4.
- asymptote when 5 - x = 0 so at x = 5.
- the negative in front of the x swings the curve so its direction is now to the left.
|
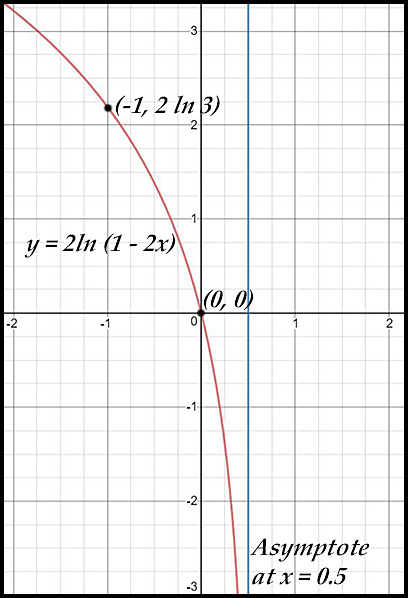
14. y = 2 loge (1 - 2x )
The curve y = 2 ln (1 - 2x) has:
- x-intercept when 1 - 2x = 1 so at x = 0.
- asymptote when 1 - 2x = 0 so at x = 0.5.
- the negative in front of the x swings the curve so its direction is now to the left.
|
| |
|
|
| |
|
|
| Combination of transformations |
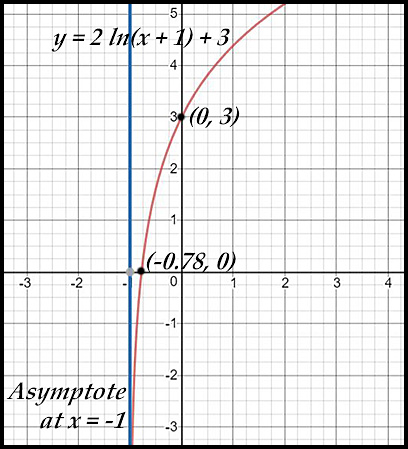
19. y = 2loge (x+1) + 3
The curve y = 2ln (x + 1) + 3 has:
- x-intercept when ln (x + 1) = -1.5 -
so when x = -1 + e-1.5 = -0.78.
- asymptote when x + 1 = 0 so at x = -1.
|
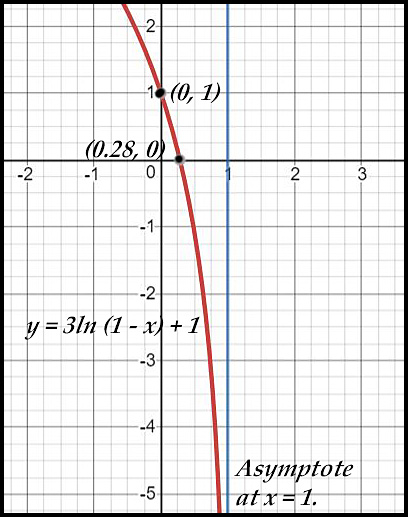
20. y = 3 ln (1 - x) + 1
The curve y = 3ln (1 - x) + 1 has:
- x-intercept when ln (1 - x) = -1/3 and then raised 1 -
so when
x = 1 - e-0.33 = 0.28.
- asymptote when 1 - x = 0 so at x = 1.
- the negative in front of the x swings the curve so its direction is now to the left.
|
| |
21. |
22. |
| Miscellaneous graphing problems. |
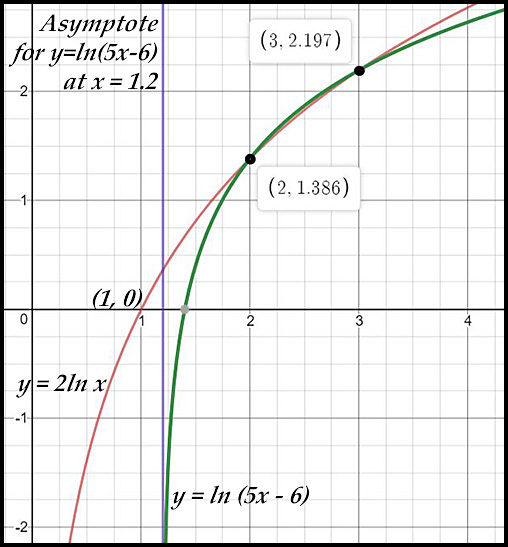
23. (i) Draw the graphs of both
y = 2 ln x and y = ln (5x - 6).
(ii) Solve the two equations simultaneously and show that your points of intersection are approximately reflected in your graph.
(i) See at right.
(ii) 2 ln x = ln x2 = ln (5x - 6)
Equating the bits after the ln:
x2 - 5x + 6 = 0
(x - 2)(x - 3) = 0
x = 2 or x = 3
x = 2, y = ln 4 = 1.386
x = 3, y = ln 9 = 2.197
|
 |
| |
24. (i) Sketch y = ln x.
(ii) By drawing a second sketch of a relevant curve on your first set of axes, find the number of solutions for the equation ln x - x = -2.
(i) See at right.
(ii) Replace ln x with y so the equation now reads y - x = -2
So y = x - 2.
Draw this line (as shown) and count the number of points of intersection.
Answer: 2
So there are 2 solutions (and we are not asked even to approximate them)  !! !! |
 |
| |
25. 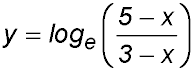 is a difficult graph to draw. is a difficult graph to draw.
- What two values of x can we see are not possible? x = 3 and x = 5.
- What about in-between 3 and 5 - say x = 4? Not possible as the log develops a negative sign for its argument.
- What about x < 3? As x gets closer to 3, the denominator becomes very small and so the value of the logarithm becomes very large. When x = 0, (5/3) > 1 so the log > 1.
As x gets more negative, the denominator is always less than the numerator
so the value of the log is always greater than 1.
- What about x > 5? The fraction has negative numerators and denominators but the denominator is always the larger value. So the value of the fraction is always positive but less than 1 - so the log is always negative.
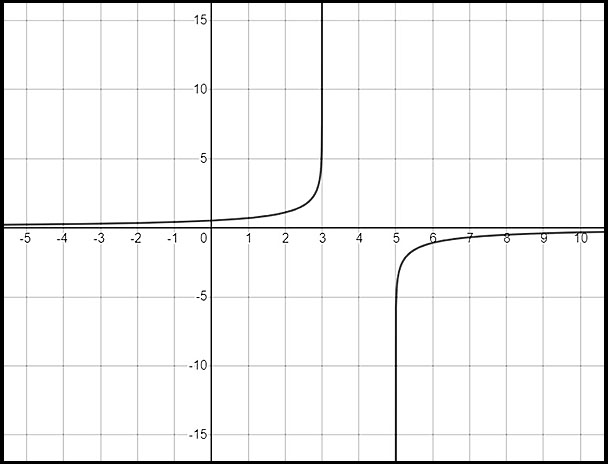
The domain is therefore (-∞, 3) and (5, ∞).
As the value of the fraction approaches 1 when x approaches 3 or 5, the value of the log must approach 0.
The range is therefore  . . |
| |
26.  |

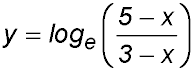 is a difficult graph to draw.
is a difficult graph to draw.